Crescimento e decrescimento

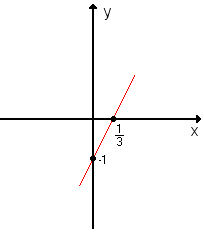
Consideremos a função do 1º grau y = 3x - 1. Vamos atribuir valores cada vez maiores a x e observar o que ocorre com y:

X -3 -2 -1 0 1 2 3 Y -10 -7 -4 -1 2 5 8 Notemos que, quando aumentos o valor de x, os correspondentes valores de y também aumentam. Dizemos, então que a função y = 3x - 1 é crescente.    Observamos novamente seu gráfico:

Regra geral:

A função do 1º grau f(x) = ax + b é crescente quando o coeficiente de x é positivo (a > 0); a função do 1º grau f(x) = ax + b é decrescente quando o coeficiente de x é negativo (a < 0);

Justificativa:

• Para a > 0: se x₁ < x₂, então ax₁ < ax₂. Daí, ax₁ + b < ax₂ + b, de onde vem f(x₁) < f(x₂).
• Para a < 0: se x₁ < x₂, então ax₁ > ax₂. Daí, ax₁ + b > ax₂ + b, de onde vem f(x₁) > f(x₂).