Estudar o sinal de qualquer y = f(x)
(função do 1º grau) é determinar os valores de x para os quais y é positivo, os
valores de x para os quais y é zero e os valores de x para os quais y é
negativo. Consideremos uma função afim y = f(x) = ax + b vamos estudar
seu sinal. Já vimos que essa função se anula pra raiz x = -b/a.
Há dois casos possíveis:
1º) a > 0 (a função é
crescente)
Y
> 0 então ax
+ b > 0 logo x > -b/a
Y
< 0 então ax + b < 0 logo x < -b/a
Conclusão: y é positivo para os valores
de x maiores que a raiz; y é negativo para os valores de x menores que a raiz.
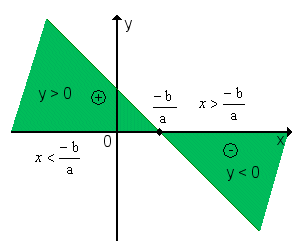
(2º) a < 0 (a função é decrescente)
Y
> 0 então ax + b > 0 logo x < -b/a
Y
< 0 então ax + b < 0 logo x > -b/a
Conclusão: y é positivo para os valores
de x menores que a raiz; y é negativo para os valores de x maiores que a
raiz.
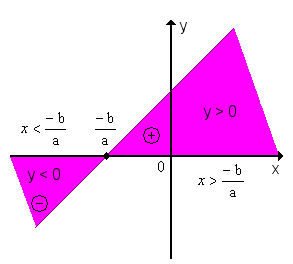
Nenhum comentário:
Postar um comentário